Answer:
The coordinates of the dillated vertices are
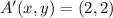 ,
,
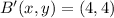 ,
,
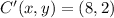 and
and
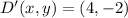 .
.
Explanation:
From Linear Algebra, we define dilation by the following equation:
![P'(x,y) = O(x,y) + k\cdot [P(x,y)-O(x,y)]](https://img.qammunity.org/2021/formulas/mathematics/college/8tvpq8lazirh3r1pcoyqnpw7jsnh7guf7w.png) (1)
(1)
Where:
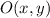 - Center of dilation, dimensionless.
- Center of dilation, dimensionless.
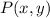 - Original point, dimensionless.
- Original point, dimensionless.
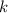 - Scale factor, dimensionless.
- Scale factor, dimensionless.
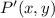 - Dilated point, dimensionless.
- Dilated point, dimensionless.
If we know that
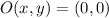 ,
,
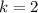 ,
,
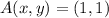 ,
,
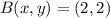 ,
,
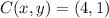 and
and
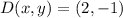 , then the dilated points are, respectively:
, then the dilated points are, respectively:
Point A
![A'(x,y) = O(x,y) + k\cdot [A(x,y)-O(x,y)]](https://img.qammunity.org/2021/formulas/mathematics/college/58b91kawxm2zyrilhgaes3594f1ghis3vz.png) (2)
(2)
![A'(x,y) = (0,0) + 2\cdot [(1,1)-(0,0)]](https://img.qammunity.org/2021/formulas/mathematics/college/g2c51yd5qmiwhf25gcjr9tc4703pvmbhr6.png)
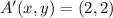
Point B
![B'(x,y) = O(x,y) + k\cdot [B(x,y)-O(x,y)]](https://img.qammunity.org/2021/formulas/mathematics/college/sjlbn74gdkj7avbshw7dznl3dxevssbqzp.png) (3)
(3)
![B'(x,y) = (0,0) + 2\cdot [(2,2)-(0,0)]](https://img.qammunity.org/2021/formulas/mathematics/college/zs0xl3h0jskzocn1udsnspjj2xc4rw2p2m.png)
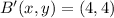
Point C
![C'(x,y) = O(x,y) + k\cdot [C(x,y)-O(x,y)]](https://img.qammunity.org/2021/formulas/mathematics/college/xg453j8s2ndbaiyw2hla34tst5dz0se83h.png)
![C'(x,y) = (0,0) + 2\cdot [(4,1)-(0,0)]](https://img.qammunity.org/2021/formulas/mathematics/college/lu7gemf1mvm8sgbbobp8md7p7g6ej0bh6v.png)
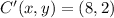
Point D
![D'(x,y) = O(x,y) + k\cdot [D(x,y)-O(x,y)]](https://img.qammunity.org/2021/formulas/mathematics/college/ptoybnq7v72qcmyejxmlqzyso36bp3p9rq.png)
![D'(x,y) = (0,0) + 2\cdot [(2,-1)-(0,0)]](https://img.qammunity.org/2021/formulas/mathematics/college/9w17w9p51rrsnomjs6k8g3s562ugwpllt3.png)
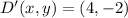
The coordinates of the dillated vertices are
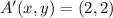 ,
,
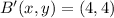 ,
,
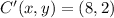 and
and
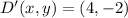 .
.