Question

A missile is moving 1350 m/s at a 25.0° angle. It needs to hit a target 23,500 m away in a 55.0° direction in 10.20 s. What is the direction of its final velocity? Answer in direction (deg)

Answer 1

(3504 m/s, 66°)

The final velocity of the missile is approximately 3504 m/s at an angle of 66 degrees.

Step-by-step explanation:

We are going to use the horizontal and vertical components of this object since it is in projectile motion.

We are given the initial velocity of the missile; 1350 m/s at an angle of 25 degrees. We are also given the displacement in the x-direction: 23,500 meters at an angle of 55 degrees. The total time of this projectile in motion is 10.20 seconds.

Using this information, we can break up the motion of the projectile into its horizontal and vertical components and solve for the unknown variables
`a` and
`v_f`.

Horizontal direction (x):

List out the known variables:

• 
  `v_i=1350`
• 
  `v_f=?`
• 
  `\triangle x=23500`
• 
  `a=?`
• 
  `t=10.20`

Since we have initial velocity, displacement, and time, we can use one of the kinematic equations for constant acceleration that contains these variables, including acceleration, and solve for a:

• 
  `\triangle x=v_it + (1)/(2)at^2`

We are solving for acceleration in the x-direction, so this equation should be in terms of the x-direction:

• 
  `\triangle x_x=(v_i)_x t +(1)/(2)a_x t^2`

Let's break up the displacement into its horizontal (x) component:

• 
  `23500cos(55)`

Let's break up the initial velocity into its horizontal component:

• 
  `1350cos(25)`

Plug these values into the equation and 10.20 seconds for t.

• 
  `23500cos(55)=1350cos(25) \cdot t + (1)/(2)a_x (10.20)^2`

Solve for
`a_x`.

• 
  `23500cos(55)=12479.85823+52.02a_x`
• 
  `999.1880243=52.02a_x`
• 
  `a_x=19.20776671`

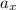The acceleration in the x-direction is about 19.21 m/s².

Now, we can use this acceleration and solve for the final velocity in the x-direction using this constant acceleration kinematic equation:

• 
  `v_f=v_i+at`

Use this equation in terms of the x-direction:

• 
  `(v_f)_x=(v_i)_x+a_xt`

Plug the known values into the equation and solve for
`(v_f)_x`.

• 
  `(v_f)_x=1350cos(55)+19.20776671 \cdot 10.20`
• 
  `(v_f)_x=1419.434733`

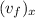The final velocity in the x-direction is about 1419.43 m/s.

Vertical direction (y):

This process will be the same as solving for acceleration and final velocity in the x-direction, except this time we will be using the vertical (y) components.

• 
  `\triangle x_y=(v_i)_y t +(1)/(2)a_y t^2`

Vertical component of initial velocity:

• 
  `1350sin(25)`

Vertical component of displacement:

• 
  `23500sin(55)`

Plug known values into the equation and solve for
`a_y`.

• 
  `23500sin(55)=1350sin(25) \cdot (10.20) + (1)/(2)a_y (10.20)^2`
• 
  `23500sin(55)=5819.453464 +52.02a_y`
• 
  `13430.61958=52.02a_y`
• 
  `a_y=258.181845`

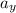The acceleration in the y-direction is about 258.18 m/s².

Now let's use the same equation we used previously to solve for the final velocity in the y-direction.

• 
  `v_f=v_i+at`

Use this equation in terms of the y-direction:

• 
  `(v_f)_y=(v_i)_y+a_y t`

Plug known values into the equation and solve for
`(v_f)_y`.

• 
  `(v_f)_y=1350sin(25)+258.181845 \cdot 10.20`

• 
  `(v_f)_y=3203.989472`

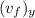The final velocity in the y-direction is about 3203.99 m/s.

Final velocity and direction:

The magnitude of the final velocity is the square root of the final velocity in the horizontal and vertical directions squared and added together.

• 
  `|v|=√((v_f)^2_x + (v_f)^2_y)`

Plug the final velocity in the x and y-directions into the equation.

• 
  `|v|=√((1419.434733)^2+(3203.989472)^2)`
• 
  `|v|=√(2014794.961+10265548.54)`
• 
  `|v|=√(12280343.5)`

• 
  `|v|=3504.332105`

The magnitude of the final velocity is about 3504 m/s. We can solve for the direction of the final velocity by using arccos to find the angle that is formed with the x-axis.

• 
  `\displaystyle\theta = cos^-^1 \big{(} (v_x)/(|v|)\big{)} }`

Plug in the x-component of the initial velocity and the magnitude of the final velocity of the projectile into the equation.

• 
  `\displaystyle \theta =cos^-^1 \big{(}(1419.434733)/(3504.332105)\big{)}}`
• 
  `\displaystyle \theta = cos^-^1 \big{(} .4050514308 \big{)}}`
• 
  `\displaystyle \theta = 66.1056499`

The direction of the final velocity is about 66 degrees.