Question

A ball with a mass of 2000 g is floating on the surface of a pool of water. What is the minimum volume that the ball could have without sinking below the surface of the water? (Note that water has a density of 1.00 g/cm³.)

Answer 1

`2000\; {\rm cm^(3)}`.

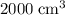Step-by-step explanation:

When the ball is placed in this pool of water, part of the ball would be beneath the surface of the pool. The volume of the water that this ball displaced is equal to the volume of the ball that is beneath the water surface.

The buoyancy force on this ball would be equal in magnitude to the weight of water that this ball has displaced.

Let
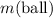`m(\text{ball})` denote the mass of this ball. Let
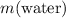`m(\text{water})` denote the mass of water that this ball has displaced.

Let
`g` denote the gravitational field strength. The weight of this ball would be
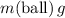`m(\text{ball}) \, g`. Likewise, the weight of water displaced would be
`m(\text{water})\, g`.

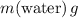For this ball to stay afloat, the buoyancy force on this ball should be greater than or equal to the weight of this ball. In other words:

`\text{buoyancy} \ge m(\text{ball})\, g`.

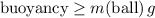At the same time, buoyancy is equal in magnitude the the weight of water displaced. Thus:

`\text{buoyancy} = m(\text{water}) \, g`.

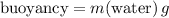Therefore:

`m(\text{water})\, g = \text{buoyancy} \ge m(\text{ball})\, g`.

`m(\text{water}) \ge m(\text{ball})`.

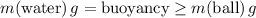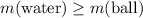In other words, the mass of water that this ball displaced should be greater than or equal to the mass of of the ball. Let
`\rho(\text{water})` denote the density of water. The volume of water that this ball should displace would be:

`\begin{aligned}V(\text{water}) &= \frac{m(\text{water})}{\rho(\text{water})} \\ &\ge \frac{m(\text{ball}))}{\rho(\text{water})} \end{aligned}`.

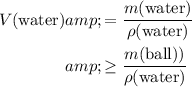Given that
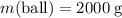`m(\text{ball}) = 2000\; {\rm g}` while
`\rho = 1.00\; {\rm g\cdot cm^(-3)}`:

`\begin{aligned}V(\text{water}) &\ge \frac{m(\text{ball}))}{\rho(\text{water})} \\ &= \frac{2000\; {\rm g}}{1.00\; {\rm g\cdot cm^(-3)}} \\ &= 2000\; {\rm cm^(3)}\end{aligned}`.

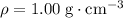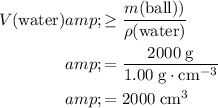In other words, for this ball to stay afloat, at least
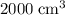`2000\; {\rm cm^(3)}` of the volume of this ball should be under water. Therefore, the volume of this ball should be at least
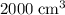`2000\; {\rm cm^(3)}\!`.