Question

There are 3 islands A,B,C. Island B is east of island A, 8 miles away. Island C is northeast of A, 5 miles away and northwest of B, 7 miles away. What is the bearing needed to navigate from island B to C? Round to the nearest degree

Answer 1

`B = 38`

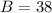
Explanation:

This question can be illustrated using the attachment and the required bearing will be calculated using cosine theorem;

`b^2 = a^2 + c^2 - 2ac\ CosB`

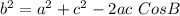
In this case:

`b = 5`

`a = 7`

`c = 8`

`<B = ??`

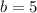
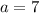
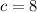
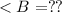
Substitute these values in
`b^2 = a^2 + c^2 - 2ac\ CosB`

`5^2 = 7^2 + 8^2 - 2 * 7 * 8\ CosB`

`25 = 49 + 64 - 112\ CosB`

`25 = 113- 112\ CosB`

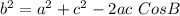
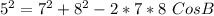
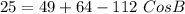
Collect Like Terms

`25 -113=- 112\ CosB`

`-88=- 112\ CosB`

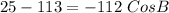
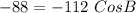
Divide through by -112

`(-88)/(-112)= (- 112\ CosB)/(-112)`

`(-88)/(-112)= CosB`

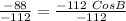
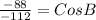
Reorder

`Cos\ B = (-88)/(-112)`

`Cos\ B = 0.7857`

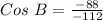
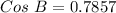
Take arccos of both sides

`B = cos^(-1)(0.7857)`

`B = cos^(-1)(0.7857)`

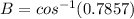
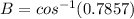
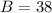`B = 38` --- (approximated)

Hence, the bearing is approximately 38 degrees