Answer:
we conclude that the function shown in the graph has a smaller rate of change and a lower starting point.
Therefore, option (A) is true.
Explanation:
FUNCTION
Given the function
y = 6x - 1
Comparing with the slope-intercept form of the graph
y = mx+b
where m is the slope and b is the y-intercept
Thus,
The slope of the function = rate of change = 6
The starting point of the function can be obtained by setting x = 0 and solve for y
i.e
at x = 0, y = 6x-1 = 6(1)-1 = 5
Thus,
The starting point of the function is (0, 5)
LINE GRAPH
Now, consider the line graph
Taking two points to find the slope
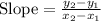
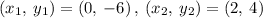

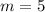
Thus,
The slope of the line graph = rate of change = 5
From the graph, it is clear that at x=0, the value of y=6
Thus,
The starting point of the graph is (0, -6)
Thus,
FOR FUNCTION
The slope of the function = rate of change = 6
The starting point of the function is (0, 5)
FOR LINE GRAPH
The slope of the line graph = rate of change = 5
The starting point of the graph is (0, -6)
Conclusion
Hence, we conclude that the function shown in the graph has a smaller rate of change and a lower starting point.
Therefore, option (A) is true.