Question

Which statement correctly compares the function shown on this graph with the function y = 6x - 1?

A. the function shown on the graph has a smaller rate of change and a lower starting point

B. the function shown on the graph has a greater rate of change and a higher starting point

C. the function shown on the graph has smaller rate of change, but a high starting point

D. the function shown on the graph has a greater rate of change and a lower starting point

Answer 1

we conclude that the function shown in the graph has a smaller rate of change and a lower starting point.

Therefore, option (A) is true.

Explanation:

FUNCTION

Given the function

y = 6x - 1

Comparing with the slope-intercept form of the graph

y = mx+b

where m is the slope and b is the y-intercept

Thus,

The slope of the function = rate of change = 6

The starting point of the function can be obtained by setting x = 0 and solve for y

i.e

at x = 0, y = 6x-1 = 6(1)-1 = 5

Thus,

The starting point of the function is (0, 5)

LINE GRAPH

Now, consider the line graph

Taking two points to find the slope

• (0, -6)

• (2, 4)

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(0,\:-6\right),\:\left(x_2,\:y_2\right)=\left(2,\:4\right)`

`m=(4-\left(-6\right))/(2-0)`

`m=5`

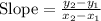
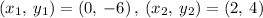
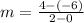
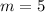
Thus,

The slope of the line graph = rate of change = 5

From the graph, it is clear that at x=0, the value of y=6

Thus,

The starting point of the graph is (0, -6)

Thus,

FOR FUNCTION

The slope of the function = rate of change = 6

The starting point of the function is (0, 5)

FOR LINE GRAPH

The slope of the line graph = rate of change = 5

The starting point of the graph is (0, -6)

Conclusion

Hence, we conclude that the function shown in the graph has a smaller rate of change and a lower starting point.

Therefore, option (A) is true.