Question

The weights of dogs at a kennel are Normally distributed with a mean of 18 pounds and a standard deviation of 3.5 pounds.In which percentile is a dog who weighs 25 pounds?

Answer 1

97.5th percentile

This is the right answer edge 2020

Explanation:

Answer 2

P(x=25)=P(z=2)=0.9972 or 99.72%

Explanation:

Mean = 18 pounds

Standard Deviation = 3.5 pounds

x= 25

We need to find P(x=25)

First, we need to find z-score using formula:
`z-score=(x-\mu)/(\sigma)`

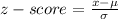
Finding z-score when x=25

`z-score=(x-\mu)/(\sigma)\\z-score=(25-18)/(3.5)\\z-score=2`

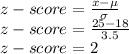
So, we need to find P(z=2)=P(x=25)

Looking at z-score table we can find P(z=2)

P(z=2)=0.9972 or 99.72%

So, P(z=2)=0.9972 or 99.72%