Question

Write an equation for the line that passes through (2,-5) and is parallel to the line 2y=3x+10

Answer 1

`y = (3)/(2) x-8`

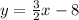
Explanation:

Firstly, let's get y by itself in the equation.

`y = (3)/(2)x + 5`

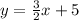
Parallel lines have the same slope, but not the same y intercept. So we have an equation like this:

`y = (3)/(2)x + b`

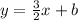
To find b (aka the y-intercept), we need to plug in the ordered pair into the equation like this:

`-5 = (3)/(2)(2) + b`

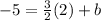
Now solve:

`-5 = (6)/(2) + b\\-5 = 3 + b\\-8 = b`

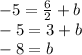
We have found the y-intercept, now we can write the full equation:

`y = (3)/(2) x-8`

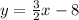
I hope this helps!!

- Kay :)