Question

Some History teachers at Riverside High School are purchasing tickets for students and their adult chaperones to go on a field trip to a nearby museum. For her class, Mrs. Levin bought 27 student tickets and 25 adult tickets, which cost a total of $614. Mr. Lawson spent $733, getting 27 student tickets and 32 adult tickets. What is the price for each type of ticket?

Answer 1

Cost of student ticket = $7

Cost of Adult ticket = $17

Explanation:

Let cost of student ticket = x

Cost of Adult ticket = y

Making expressions from statements

Mrs. Levin bought 27 student tickets and 25 adult tickets, which cost a total of $614.
`27x+25y=614`

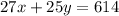
Mr. Lawson spent $733, getting 27 student tickets and 32 adult tickets.
`27x+32y=733`

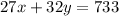
Now solving these equations to find values of x and y

Let

`27x+25y=614--eq(1)\\27x+32y=733--eq(2)`

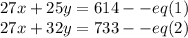
Subtracting both equations

`27x+25y=614\\27x+32y=733\\-\:\:\:-\:\:\:\:\:\:\:\:\:\:\:\:-\\-------\\-7y=-119\\y=(-119)/(-7)\\y=17`

So, we get value of y = 17

Now, finding value of x, by putting value of y in eq(1)

`27x+25y=614\\Put\:y=17\\27x+25(17)=614\\27x+425=614\\27x=614-425\\27x=189\\x=(189)/(27)\\x=7`

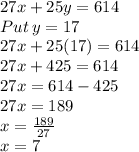
So, we get value of x = 7

Cost of student ticket = x = $7

Cost of Adult ticket = y = $17