Question

Select the correct answer​

Answer 1

a) We get
`\mathbf{A+B=x^2-2x+1}`

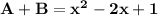
So, Is the result of A+B is a polynomial:Yes

b) We get
`\mathbf{A-B=6x^3-7x^2+2x-1}`

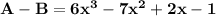
So, Is the result of A-B is a polynomial:Yes

c) We get
`\mathbf{A.B=9x^6+21x^5-18x^4+9x^3-3x^2}`

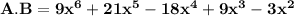
So, Is the result of A.B is a polynomial:Yes

Explanation:

We are giving the polynomial equations:

`A= 3x^2(x-1)\\B=-3x^3+4x^2-2x+1`

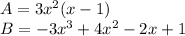
We need to find

a) A+B

`A+B=3x^2(x-1)+(-3x^3+4x^2-2x+1)\\A+B=3x^3-3x^2-3x^3+4x^2-2x+1\\A+B=3x^3-3x^3-3x^2+4x^2-2x+1\\A+B=x^2-2x+1\\`

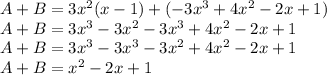
So, we get
`\mathbf{A+B=x^2-2x+1}`

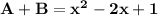
So, Is the result of A+B is a polynomial:Yes

b) A-B

`A-B=3x^2(x-1)-(-3x^3+4x^2-2x+1)\\A-B=3x^3-3x^2+3x^3-4x^2+2x-1\\A-B=3x^3+3x^3-3x^2-4x^2+2x-1\\A-B=6x^3-7x^2+2x-1\\`

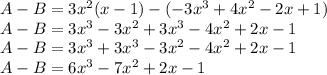
So, we get
`\mathbf{A-B=6x^3-7x^2+2x-1}`

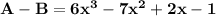
So, Is the result of A-B is a polynomial:Yes

c) A . B

`A.B=3x^3(-3x^3+4x^2-2x+1)-3x^2(-3x^3+4x^2-2x+1)\\A.B=9x^6+12x^5-6x^4+3x^3+9x^5-12x^4+6x^3-3x^2\\A.B=9x^6+12x^5+9x^5-6x^4-12x^4+3x^3+6x^3-3x^2\\A.B=9x^6+21x^5-18x^4+9x^3-3x^2`

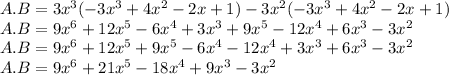
So, we get
`\mathbf{A.B=9x^6+21x^5-18x^4+9x^3-3x^2}`

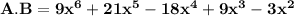
So, Is the result of A.B is a polynomial:Yes