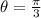Question

asked Sep 25, 2021 178k views

2 Answers

Schadensbegrenzer · Answer 1 · 2021-09-30T12:30:12+0000

Answer:

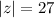|z| = 27 -- Modulus

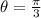$\theta = (\pi)/(3)$ --- Argument

Explanation:

Given

$((\sqrt 3)(cos(\pi)/(18) + i\ sin(\pi)/(18)))^6$

Required

Determine the modulus and the argument

We have that:

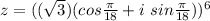
$z = ((\sqrt 3)(cos(\pi)/(18) + i\ sin(\pi)/(18)))^6$

Expand:

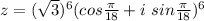
$z = (\sqrt 3)^6(cos(\pi)/(18) + i\ sin(\pi)/(18))^6$

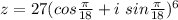
$z = 27(cos(\pi)/(18) + i\ sin(\pi)/(18))^6$

A complex equation can be expressed as:

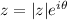
$z = |z| e^(i\theta)$

Where

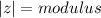
|z| = modulus

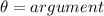
$\theta = argument$

Where

$e^(i\theta) = (cos(\pi)/(18) + i\ sin(\pi)/(18))$

So:

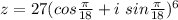$z = 27(cos(\pi)/(18) + i\ sin(\pi)/(18))^6$ becomes

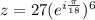
$z = 27(e^{i(\pi)/(18)})^6$

By comparison:

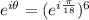
$e^(i\theta) = (e^{i(\pi)/(18)})^6$

This gives:

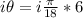
${i\theta} = i(\pi)/(18)}*6$

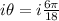
${i\theta} = i(6\pi)/(18)}$

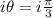
${i\theta} = i(\pi)/(3)}$

Divide through by i

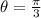
$\theta = (\pi)/(3)$

Hence, the modulus, z is:

|z| = 27

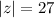
And the argument
$\theta$ is

$\theta = (\pi)/(3)$

Please log in or register to add a comment.