Question

Which statements verify that the solution set to |x + 3| < 5 is –8 < x < 2? Check all that apply. Substituting a value into the inequality from the solution set, such as –2, will create a true statement. Substituting a value into the inequality from the solution set, such as 1, will create a false statement. Substituting a value into the inequality not from the solution set, such as 4, will create a true statement. Substituting a value into the inequality not from the solution set, such as 6, will create a false statement. Substituting any value into the inequality will create a true statement.

Answer 1

First and fourth statements are correct

Explanation:

The function is
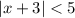`|x+3|<5` where the domain is
`-8<x<2`

`|-2+3|=1<5`

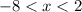
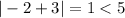
The first statement is correct.

`|1+3|=4<5`

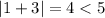
Substituting a value into the inequality from the solution set, such as 1, will create a false statement. This is wrong as it creates a true statement.

`|4+3|=7\\less 5`

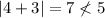
Substituting a value into the inequality not from the solution set, such as 4, will create a true statement. This is wrong as a value which is not from the solution set will create a false statement.

`|6+3|=9\\less 5`

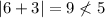
Substituting a value into the inequality not from the solution set, such as 6, will create a false statement. This is correct.

`|10+3|=13\\less 5`

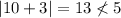
Substituting any value into the inequality will create a true statement. This is wrong as the value of x must be in the solution set.