Question

The real numbers x and y satisfy the equations:

xy - x = 180 and y + xy = 208.
Let the two solutions be (x1, y1 and (x2, y2).
What is the value of x1 + 10y1 + x2 + 10y2

Answer 1

The value of
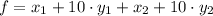`f = x_(1)+10\cdot y_(1)+x_(2)+10\cdot y_(2)` is 317.

Explanation:

Let the system of nonlinear equations be:

`x\cdot (y-1) = 180` (1)

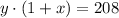`y\cdot (1+x) = 208` (2)

From (1), we clear
`x`:

`x = (180)/(y-1)`

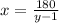
Let apply this resulting expression in (2):

`y\cdot \left(1+(180)/(y-1) \right)= 208`

`y\cdot \left((y-1+180)/(y-1) \right) = 208`

`y\cdot \left((y+179)/(y-1) \right)=208`

`y\cdot (y+179) = 208\cdot (y-1)`

`y^(2)+179\cdot y = 208\cdot y-208`

`y^(2)-29\cdot y+208 = 0`

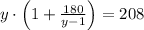
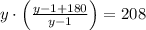
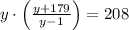
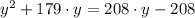
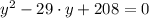
By the Quadratic Formula we obtain the solution of the second order polynomial:

`y_(1) = 16` and
`y_(2) = 13`

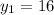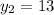
And the respective values of
`x` are, respectively:

`y_(1) = 16`

`x_(1) = (180)/(y_(1)-1)`

`x_(1) = (180)/(15)`

`x_(1) = 12`

`y_(2) = 13`

`x_(2) = (180)/(y_(2)-1)`

`x_(2) = (180)/(12)`

`x_(2) = 15`

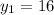
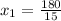
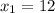
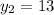
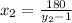
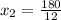
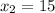
If we know that
`x_(1) = 12`,
`y_(1) = 16`,
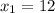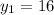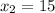`x_(2) = 15` and
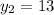`y_(2) = 13`, then the value of
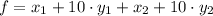`f = x_(1)+10\cdot y_(1)+x_(2)+10\cdot y_(2)` is:

`f = 12+10\cdot (16)+15+10\cdot (13)`

`f = 317`

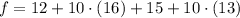
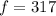
The value of
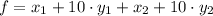`f = x_(1)+10\cdot y_(1)+x_(2)+10\cdot y_(2)` is 317.