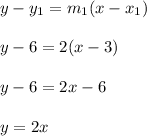Question

Lines a, b, and c lie on the same coordinate plane. Line a is perpendicular to line b and intersects at (3, 6). Line b is perpendicular to line c, which is the graph of y = 2x + 3.

Write the equations of lines a and b.

Answer 1

The answer is below

Explanation:

The equation of a straight line is given as y = mx + b, where m is the slope and b is the y intercept.

Given that the equation of line c is y = 2x + 3, and line b is perpendicular to line c. Two lines are perpendicular if the product of their slope is -1. We can see that the slope of line c is 2, let
`m_1` be the slope of line c, hence:

`2*m_1=-1\\\\m_1=(-1)/(2)`

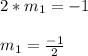
Also, line b passes through (3, 6), hence the equation of line b is:

`y-y_1=m_1(x-x_1)\\\\y-6=(-1)/(2)(x-3)\\\\y-6= (-1)/(2)x+(3)/(2)\\\\y=(-1)/(2)x+ (15)/(2)`

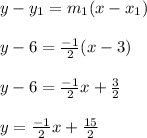
Line b has a slope of -1/2, and is perpendicular to line a, let
`m_2` be the slope of line a, hence:

`(-1)/(2) *m_2=-1\\\\m_2=2`

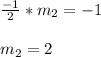
Also, line a passes through (3, 6), hence the equation of line a is:

`y-y_1=m_1(x-x_1)\\\\y-6=2(x-3)\\\\y-6=2x-6\\\\y=2x`