Question

What fraction of an iceberg is submerged? (ρice = 917 kg/m3, ,ρsea = 1030 kg/m3.)

Answer 1

Choice d. Approximately
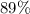`89\%` of the volume of this iceberg would be submerged.

Step-by-step explanation:

Let
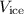`V_\text{ice}` denote the total volume of this iceberg. Let
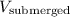`V_\text{submerged}` denote the volume of the portion that is under the liquid.

The mass of that iceberg would be
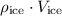`\rho_\text{ice} \cdot V_\text{ice}`. Let
`g` denote the gravitational field strength (
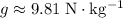`g \approx 9.81\; \rm N \cdot kg^(-1)` near the surface of the earth.) The weight of that iceberg would be:
`\rho_\text{ice} \cdot V_\text{ice} \cdot g`.

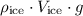If the iceberg is going to be lifted out of the sea, it would take water with volume
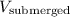`V_\text{submerged}` to fill the space that the iceberg has previously taken. The mass of that much sea water would be
`\rho_\text{sea} \cdot V_\text{submerged}`.

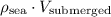Archimedes' Principle suggests that the weight of that much water will be exactly equal to the buoyancy on the iceberg. By Archimedes' Principle:

`\text{buoyancy} = \rho_\text{sea} \cdot V_\text{submerged} \cdot g`.

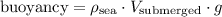The buoyancy on the iceberg should balance the weight of this iceberg. In other words:

`\underbrace{\rho_\text{ice} \cdot V_\text{ice} \cdot g}_\text{weight of iceberg} = \underbrace{\rho_\text{sea} \cdot V_\text{submerged} \cdot g}_\text{buoyancy on iceberg}`.

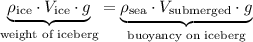Rearrange this equation to find the ratio between
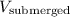`V_\text{submerged}` and
`V_\text{ice}`:

`\begin{aligned} &\frac{V_\text{submerged}}{V_\text{ice}} \\&= \frac{\rho_\text{ice} \cdot g}{\rho_\text{sea} \cdot g}\\ &= \frac{\rho_\text{ice}}{\rho_\text{sea}}\ = (917\; \rm kg \cdot m^(-3))/(1030\; \rm kg \cdot m^(-3)) \approx 0.89 \end{aligned}`.

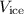In other words,
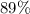`89\%` of the volume of this iceberg would have been submerged for buoyancy to balance the weight of this iceberg.