Question

Suppose that the functions q and r are defined as follows.

g(x)=x² +5
r(x)=√x+7
Find the following.
(roq)(2) = 0
&
X
(q or)(2) =
5
?

Answer 1

(r o g)(2) = 4

(q o r)(2) = 14

Explanation:

Given

`g(x) = x^2 + 5`

`r(x) = √(x + 7)`

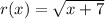
Solving (a): (r o q)(2)

In function:

(r o g)(x) = r(g(x))

So, first we calculate g(2)

`g(x) = x^2 + 5`

`g(2) = 2^2 + 5`

`g(2) = 4 + 5`

`g(2) = 9`

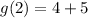
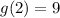
Next, we calculate r(g(2))

Substitute 9 for g(2)in r(g(2))

r(q(2)) = r(9)

This gives:

`r(x) = √(x + 7)`

`r(9) = \sqrt{9 +7{`

`r(9) = √(16)`{

`r(9) = 4`

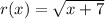
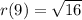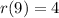
Hence:

(r o g)(2) = 4

Solving (b): (q o r)(2)

So, first we calculate r(2)

`r(x) = √(x + 7)`

`r(2) = √(2 + 7)`

`r(2) = √(9)`

`r(2) = 3`

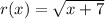
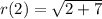
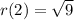
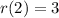
Next, we calculate g(r(2))

Substitute 3 for r(2)in g(r(2))

g(r(2)) = g(3)

`g(x) = x^2 + 5`

`g(3) = 3^2 + 5`

`g(3) = 9 + 5`

`g(3) = 14`

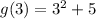
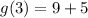
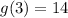
Hence:

(q o r)(2) = 14