Answer:
The value of
 is -9.
is -9.
Explanation:
If
 ,
,
 and
and
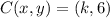 , then
, then
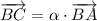 . By vectors sum, we find each vector below:
. By vectors sum, we find each vector below:
 (1)
(1)
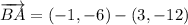
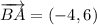
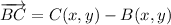 (2)
(2)
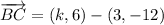
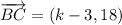
By substituting in the equation defined at the begining of this answer:
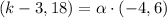
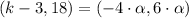 (3)
(3)
The value of
 is:
is:
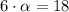 (3a)
(3a)
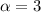
If we know that
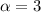 , then the value of
, then the value of
 is:
is:
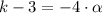


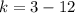

Then, the value of
 is -9.
is -9.