Question

Suppose that the functions q and r are defined as follows.

q (x)=–2x+1
r(x) = 2x²+2
Find the following.
(r og)(-1) = 0
0/6
Х
(q or)(-1) = 0
5
?

Answer 1

(r o q)(-1) = 20

(q o r)(-1) = -11

Explanation:

Given

`q(x) = -2x + 1`

`r(x) = 2x^2 + 2`

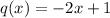
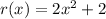
Solving (a): (r o q)(-1)

In function:

(r o q)(x) = r(q(x))

So, first we calculate q(-1)

`q(x) = -2x + 1`

`q(-1) = -2(-1) + 1`

`q(-1) = 2 + 1`

`q(-1) = 3`

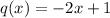
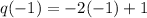
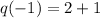
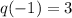
Next, we calculate r(q(-1))

Substitute 3 for q(-1)in r(q(-1))

r(q(-1)) = r(3)

This gives:

`r(x) = 2x^2 + 2`

`r(3) = 2(3)^2 + 2`

`r(-1) = 2*9 + 2`

`r(-1) = 20`

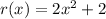
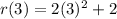
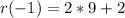
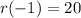
Hence:

(r o q)(-1) = 20

Solving (b): (q o r)(-1)

So, first we calculate r(-1)

`r(x) = 2x^2 + 2`

`r(-1) = 2(-1)^2 + 2`

`r(-1) = 2*1 + 2`

`r(-1) = 6\\`

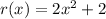
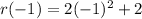
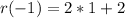
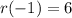
Next, we calculate r(q(-1))

Substitute 6 for r(-1)in q(r(-1))

q(r(-1)) = q(6)

`q(x) = -2x + 1`

`q(6) = -2(6) + 1`

`q(6) =- 12 + 1`

`q(6) = -11`

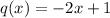
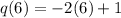
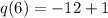
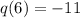
Hence:

(q o r)(-1) = -11