Question

A 100 g ball collides elastically with a 300 g ball that is at rest. If the 100 g ball was traveling

in the positive x-direction at 6.20 m/s before the
collision, what are the velocities of the two
balls after the collision?

Answer 1

The magnitude of the velocities of the two balls after the collision is 3.1 m/s (each one).

Step-by-step explanation:

We can find the velocity of the two balls after the collision by conservation of linear momentum and energy:

`P_(1) = P_(2)`

`m_(1)v_{1_(i)} + m_(2)v_{2_(i)} = m_(1)v_{1_(f)} + m_(2)v_{2_(f)}`

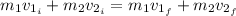
Where:

m₁: is the mass of the ball 1 = 100 g = 0.1 kg

m₂: is the mass of the ball 2 = 300 g = 0.3 kg

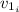`v_{1_(i)}`: is the initial velocity of the ball 1 = 6.20 m/s

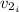`v_{2_(i)}`: is the initial velocity of the ball 2 = 0 (it is at rest)

`v_{1_(f)}`: is the final velocity of the ball 1 =?

`v_{2_(f)}`: is the initial velocity of the ball 2 =?

`m_(1)v_{1_(i)} = m_(1)v_{1_(f)} + m_(2)v_{2_(f)}`

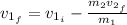`v_{1_(f)} = v_{1_(i)} - \frac{m_(2)v_{2_(f)}}{m_(1)}` (1)

Now, by conservation of kinetic energy (since they collide elastically):

`(1)/(2)m_(1)v_{1_(i)}^(2) = (1)/(2)m_(1)v_{1_(f)}^(2) + (1)/(2)m_(2)v_{2_(f)}^(2)`

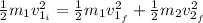
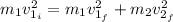`m_(1)v_{1_(i)}^(2) = m_(1)v_{1_(f)}^(2) + m_(2)v_{2_(f)}^(2)` (2)

By entering equation (1) into (2) we have:

`m_(1)v_{1_(i)}^(2) = m_(1)(v_{1_(i)} - \frac{m_(2)v_{2_(f)}}{m_(1)})^(2) + m_(2)v_{2_(f)}^(2)`

`0.1 kg*(6.20 m/s)^(2) = 0.1 kg*(6.2 m/s - \frac{0.3 kg*v_{2_(f)}}{0.1 kg})^(2) + 0.3 kg(v_{2_(f)})^(2)`

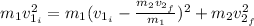
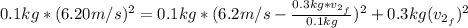
By solving the above equation for
`v_{2_(f)}`:

`v_{2_(f)} = 3.1 m/s`

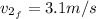
Now,
`v_{1_(f)}` can be calculated with equation (1):

`v_{1_(f)} = 6.20 m/s - (0.3 kg*3.1 m/s)/(0.1 kg) = -3.1 m/s`

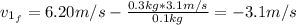
The minus sign of
`v_{1_(f)}` means that the ball 1 (100g) is moving in the negative x-direction after the collision.

Therefore, the magnitude of the velocities of the two balls after the collision is 3.1 m/s (each one).

I hope it helps you!