Question

Please help please help please help please help please help please help look at the thingy pls help

Answer 1

The slopes of line segments AC and AD are same or constant i.e
`(1)/(3)`

Explanation:

We need to find slopes of AC and AD and tell if they are same or not.

The formula used to calculate slope is:
`Slope=(y_2-y_1)/(x_2-x_1)`

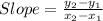
Finding slope of AC

We have A=(3,2) and C=(0,1)

Finding slope using formula:

We have
`x_1=3, y_1=2, x_2=0,y_2=1`

`Slope=(y_2-y_1)/(x_2-x_1)\\Slope=(1-2)/(0-3)\\Slope=(-1)/(-3)\\Slope=(1)/(3)`

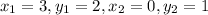
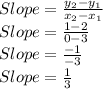
So, Slope of AC is
`(1)/(3)`

Finding slope of AD

We have A=(3,2) and C=(9,4)

Finding slope using formula:

We have
`x_1=3, y_1=2, x_2=9,y_2=4`

`Slope=(y_2-y_1)/(x_2-x_1)\\Slope=(4-2)/(9-3)\\Slope=(2)/(6)\\Slope=(1)/(3)`

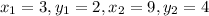
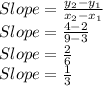
So, Slope of AD is
`(1)/(3)`

So, the slopes of line segments AC and AD are same or constant i.e
`(1)/(3)`