Question

A water-skier of mass 75.0 kg initially at rest is being pulled due east by a horizontal towrope. The rope exerts a force of 365 N (east). The water (and air) exerts a combined average frictional force of 190 N (in the opposite direction). How fast will the skier be moving after a distance of 38.0 m?

Answer 1

The skier will be moving at 13.31 m/s.

Step-by-step explanation:

To calculate the velocity of the skier we need to find the acceleration, as follows:

`\Sigma F = ma`

`F_(r) - F_(f) = ma`

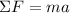
Where:

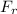`F_(r)`: is the force due to the rope = 365 N

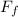`F_(f)`: is the combined average frictional force = 190 N

m: is the mass = 75.0 kg

`a = (365 N - 190 N)/(75.0 kg) = 2.33 m/s^(2)`

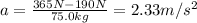
Now, we can calculate the velocity of the skier by using the following kinematic equation:

`v_(f)^(2) = v_(0)^(2) + 2ad`

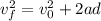
Where:

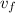`v_(f)`: is the final velocity =?

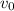`v_(0)`: is the initial velocity = 0 (the skier is initially at rest)

d: is the distance = 38.0 m

`v_(f) = \sqrt{2*2.33 m/s^(2)*38.0 m} = 13.31 m/s`

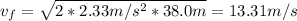
Therefore, the skier will be moving at 13.31 m/s.

I hope it helps you!