Answer:
Shifts 4 units down --->
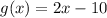
Stretches f(x) by a factor of 4 away from x-axis--->
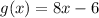
Shifts f(x) 4 units right--->
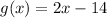
Compress f(x) by a factor of 1/4 toward the y-axis --->
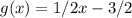
Explanation:
We are given
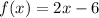
We need to match the transformations.
1) shifts f(x) 4 units down.
When function f(x) shifts k units down the new function becomes f(x)-k
In our case
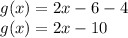
So, Shifts 4 units down --->
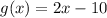
2) Stretches f(x) by a factor of 4 away from x-axis
When function f(x) is stretched by a factor of b away from x-axis the new function becomes f(bx)
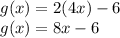
So, Stretches f(x) by a factor of 4 away from x-axis--->
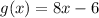
3) Shifts f(x) 4 units right
When function f(x) shifts h units right the new function becomes f(x-h)
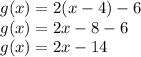
So, Shifts f(x) 4 units right--->
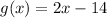
4) Compress f(x) by a factor of 1/4 toward the y-axis
When function f(x) is compressed by h factor of a toward the y-axis the new function becomes h.f(x)
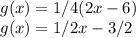
Compress f(x) by a factor of 1/4 toward the y-axis --->
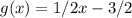
(Option Not given)
(If we compress f(x) by a factor of 4 towards y-axis we get g(x)=8x-24)