Answer:
Please check the explanation.
Explanation:
Let us consider
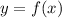
To find the area under the curve
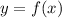 between
between
 and
and
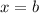 , all we need is to integrate
, all we need is to integrate
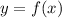 between the limits of
between the limits of
 and
and
 .
.
For example, the area between the curve y = x² - 4 and the x-axis on an interval [2, -2] can be calculated as:
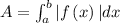
=
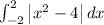
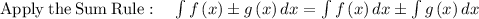
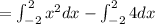
solving

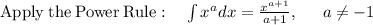
![=\left[(x^(2+1))/(2+1)\right]^2_(-2)](https://img.qammunity.org/2021/formulas/mathematics/college/a2q4qon78beci2a7wj34puioi4w5voi83g.png)
![=\left[(x^3)/(3)\right]^2_(-2)](https://img.qammunity.org/2021/formulas/mathematics/college/pl2iaeoefijkpzrqzbgoaqruis2atc7jwo.png)
computing the boundaries
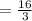
Thus,

similarly solving
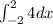
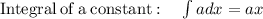
![=\left[4x\right]^2_(-2)](https://img.qammunity.org/2021/formulas/mathematics/college/8rhahbshjp1k1ff36u58yzp1rizzj9o3b3.png)
computing the boundaries
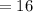
Thus,
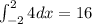
Therefore, the expression becomes
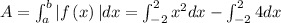

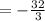
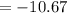 square units
square units
Thus, the area under a curve is -10.67 square units
The area is negative because it is below the x-axis. Please check the attached figure.