Answer:
The required polynomial is:
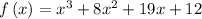
Explanation:
Given the zeros
-4, -1, -3
Zeros can be written as:
x = -4, x = -1, x = -3
Finding the factors
x = -4
x +4 = 0
x = -1
x + 1 = 0
x = -3
x + 3 = 0
Thus, the factor are:
(x+4) (x+1) (x+3)
The original function can be computed by multiplying the factors
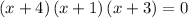
as
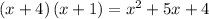
so the expression becomes
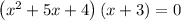
Distribute parentheses
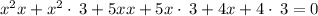
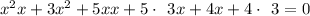
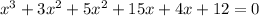
Add similar elements:

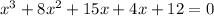
Add similar elements:

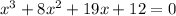
Thus, the required polynomial is:
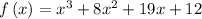
Note: your answer choices are a little ambiguous, but I have explained the entire procedure. Hopefully, it will clear your concept.