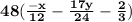Answer:
Combining and simplifying
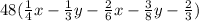 we get
we get
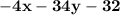 or we can write as
or we can write as
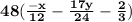
Explanation:
We need to combine and simplify
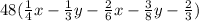
First we will combine like terms and then perform the mathematical operations like addition or subtraction.
Like terms: terms having same variable

Now we take LCM of like terms
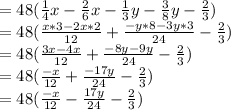
Now, we can multiply 48 with terms inside the bracket.
we can simplify the terms if they are both divisible by same number.
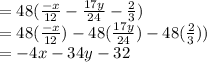
So, Combining and simplifying
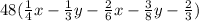 we get
we get
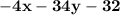 or we can write as
or we can write as