Question

How do I use the Descartes Rule of Signs to determine all possible number of positive and negative zeros?

f(x)= x^4-2x^3-4x^2+2x+3​

Answer 1

We conclude that:

• 2 or 0 positive real roots

• 2 or 0 negative real roots

Explanation:

Descartes Rule states that if the terms of a single-variable polynomial with real coefficients are ordered by descending variable exponent, then the number of positive roots of the polynomial is:

• Either equal to the number of sign differences between consecutive nonzero coefficients,

• Or is less than it by an even number.

Given the function

`f\left(x\right)=x^4-2x^3-4x^2+2x+3`

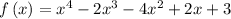
So, the coefficients are 1, −2, −4, 2, 3

As can be seen, there are 2 changes.

This means that there are 2 or 0 positive real roots.

To find the number of negative real roots, substitute x with -x in the given polynomial:

`x^4-2x^3-4x^2+2x+3` becomes
`x^4+2x^3-4x^2-2x+3`

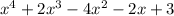
The coefficients are 1, 2, −4, −2, 3

As can be seen, there are 2 changes.

This means that there are 2 or 0 negative real roots.

Therefore, we conclude that:

• 2 or 0 positive real roots

• 2 or 0 negative real roots