Question

The first three terms of an arithmetic series are 6p+2, 4p²-10 and 4p+3 respectively. Find the possible values of p. Calculate the common difference for each value of p.​

Answer 1

First Case:

`\displaystyle p=(5)/(2)\text{ and } d=-2`

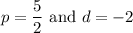
Second Case:

`\displaystyle p=-(5)/(4)\text{ and } d=(7)/(4)`

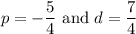
Explanation:

We know that the first three terms of an arithmetic series are:

`6p+2, 4p^2-10, \text{ and } 4p+3`

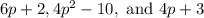
Since this is an arithmetic sequence, each subsequent term is d more than the previous term, where d is our common difference.

Therefore, we can write the second term as;

`4p^2-10=(6p+2)+d`

And, likewise, for the third term:

`4p+3=(6p+2)+2d`

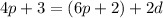
Let's solve for d for each of the equations.

Subtracting in the first equation yields:

`d=4p^2-6p-12`

And for the second equation:

`2d=-2p+1`

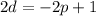
To avoid fractions, let's multiply the first equation by 2. Hence:

`2d=8p^2-12p-24`

Therefore:

`8p^2-12p-24=-2p+1`

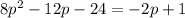
Simplifying yields:

`8p^2-10p-25=0`

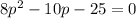
Solve for p. We can factor:

`8p^2+10p-20p-25=0`

Factor:

`2p(4p+5)-5(4p+5)=0`

Grouping:

`(2p-5)(4p+5)=0`

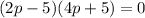
Zero Product Property:

`\displaystyle p_1=(5)/(2) \text{ or } p_2=-(5)/(4)`

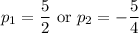
Then, we can use the second equation to solve for d. So:

`2d_1=-2p_1+1`

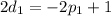
Substituting:

`\begin{aligned} 2d_1&=-2((5)/(2))+1 \\ 2d_1&=-5+1 \\ 2d_1&=-4 \\ d_1&=-2\end{aligned}`

So, for the first case, p is 5/2 and d is -2.

Likewise, for the second case:

`\begin{aligned} 2d_2&=-2(-(5)/(4))+1 \\ 2d_2&=(5)/(2)+1 \\ 2d_2&=(7)/(2) \\ d_2&=(7)/(4)\end{aligned}`

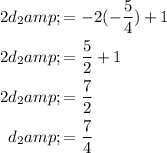
So, for the second case, p is -5/4, and d is 7/4.

By using the values, we can determine our series.

For Case 1, we will have:

17, 15, 13.

For Case 2, we will have:

-11/2, -15/4, -2.