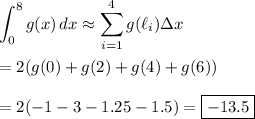Question

Using a left endpoint riemann sum approximation with four equal subintervals, the approximate value of integral from 0 to 8 g(x) dx is:​

Answer 1

Subdividing [0, 8] into 4 equally-spaced subintervals, each one will have length ∆x = (8 - 0)/4 = 2, and the partition is

[0, 2] U [2, 4] U [4, 6] U [6, 8]

We approximate the integral with a left endpoint sum. The left endpoint of the i-th subinterval is

`\ell_i = 2(i-1)`

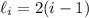
where 1 ≤ i ≤ 4.

Then the integral is approximated by

`\displaystyle \int_0^8 g(x) \, dx \approx \sum_(i=1)^4 g(\ell_i) \Delta x \\\\ = 2 (g(0) + g(2) + g(4) + g(6)) \\\\ = 2 (-1 - 3 - 1.25 - 1.5) = \boxed{-13.5}`