Question

Evaluate the definite integral from pi/2 to put of cos theta/sqrt 1+ sin theta.​

Answer 1

`\textsf{B.}\quad -2(√(2)-1)`

Explanation:

Given integral:

`\displaystyle \int^(\pi)_{(\pi)/(2)}(\cos \theta)/(√(1+ \sin \theta))\:\:d\theta`

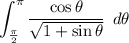
Solve by using Integration by Substitution

Substitute u for one of the functions of
`\theta` to give a function that's easier to integrate.

`\textsf{Let }u=1+\sin \theta`

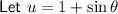
Find the derivative of u and rewrite it so that
`d \theta` is on its own:

`\implies (du)/(d \theta)=\cos \theta`

`\implies d \theta=(1)/(\cos \theta)\:du`

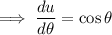
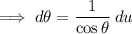
Use the substitution to change the limits of the integral from
`\theta`-values to u-values:

`\textsf{When }\theta=\pi \implies u=1`

`\textsf{When }\theta=(\pi)/(2) \implies u=2`

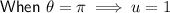
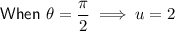
Substitute everything into the original integral and solve:

`\begin{aligned}\displaystyle \int^(\pi)_{(\pi)/(2)}(\cos \theta)/(√(1+ \sin \theta))\:\:d\theta & =\int^(1)_2}(\cos \theta)/(√(u))\:\cdot (1)/(\cos \theta)\:\:du\\\\& =\int^(1)_(2)(1)/(√(u)) \:\:du \\\\& =\int^(1)_(2) u^{-(1)/(2)}\:\:du \\\\& = \left[ 2u^{(1)/(2)} \right]^(1)_(2)\\\\& = \left(2(1)^{(1)/(2)}\right)-\left(2(2)^{(1)/(2)}\right)\\\\& = 2-2√(2)\\\\& = -2(√(2)-1)\end{aligned}`