-------------------------------------------------------------------------------------------------------------
Answer:

-------------------------------------------------------------------------------------------------------------
Given:
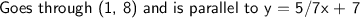
Find:

Solution: We know that our equation is going to parallel to the line that was given therefore the slope would stay the same at 5/7. We also have a point so we can plug in the values into the point-slope form, distribute, and solve for y.
Plug in the values
Distribute
Add 8 to both sides
Therefore, the final equation that follows the description that was provided in the problem statement is y = 5/7x + 51/7.