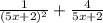Explanation:
We have
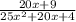
Let's factor the denomiator first,
the denomaitor is a perfect square so we get

Now, we must think of two fractions that
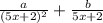
We use a perfect square term for one fraction, then a linear one for the next, because if we set both of the denomiator to the same factor, we would get a inconsistent system.
So right now, we have
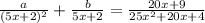
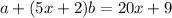
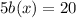
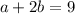
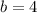
so that means that a is
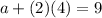
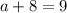
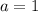
So our equation is