Question

What is the completely factored form of this polynomial? 2x5 + 12x3 − 54x

Answer 1

2x(x^2 - 3)(x^2 + 9)

Explanation:

2x^5 + 12x^3 − 54x

2x(x^4 + 6x - 27)

Since -3 + 9 = 6 and -3 x 9 = -27:

2x(x^2 - 3)(x^2 + 9)

Answer 2

`2x(x^2-3)(x^2+9)`

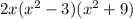
Explanation:

Given polynomial:

`2x^5+12x^3-54x`

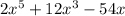
Factor out the common term
`2x`:

`\implies 2x(x^4+6x^2-27)`

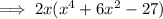
To factor the trinomial
`x^4+6x^2-27`:

`\textsf{Let }u=x^2 \implies u^2+6u-27`

Factor the quadratic by finding two numbers that multiply to -27 and sum to 6: 9 and -3

Rewrite the middle term as the sum of these two numbers:

`\implies u^2+9u-3u-27`

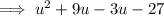
Factorize the first two terms and the last two terms separately:

`\implies u(u+9)-3(u+9)`

Factor out the common term (u + 9):

`\implies (u-3)(u+9)`

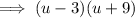
Substitute back
`u=x^2`:

`\implies (x^2-3)(x^2+9)`

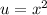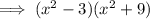
Therefore, the factored form of the given polynomial is:

`\implies 2x(x^2-3)(x^2+9)`