Question

Anyone know how to solve this?

Answer 1

ya we have to tell its initial value after 11 years it too simple

Answer 2

The value after 11 years would be: 2880 us dollars

Explanation:

Given the function

`v\left(t\right)=32,000\left(0.80\right)^t`

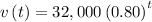
The initial value is basically the first output value when the input value = 0.

Here,

The initial value can be obtained by putting t=0 in the function

`v\left(0\right)=32,\:000\left(0.80\right)^0`

`\mathrm{Apply\:rule}\:a^0=1,\:a\\e \:0`

`0.8^0=1`

Thus,

`v\left(0\right)=32000\cdot \:\:1`

`=32000`

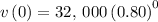
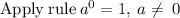
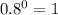
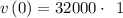
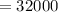
Thus, initial value = v(0) = 32000

Value after 11 years can be obtained by putting t=11 in the function

`v\left(11\right)=32,\:000\left(0.80\right)^(11)`

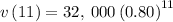
as

`0.8^(11)=0.09`

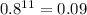
so the expression becomes

`v(11)=32000\cdot \:\:0.09`

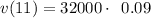
`=2880` us dollars

Thus, the value after 11 years would be: 2880 us dollars