Answer:
NOT a single ordered pair satisfies the equation.
Explanation:
Given the equation
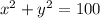
Let us substitute all the given ordered pairs to find which ordered pair satisfies the equation.
For (0, -100)
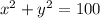
substitute x=0 and y=-100
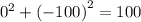
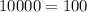
FALSE
Thus, the ordered pair (0, -100) does NOT satisfy the equation.
For (10, -10)
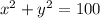
substitute x=10 and y=-10
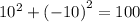
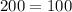
FALSE
Thus, the ordered pair (10, -10) does NOT satisfy the equation.
For (25, 75)
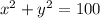
substitute x=25 and y=75
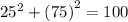
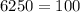
FALSE
Thus, the ordered pair (25, 75) does NOT satisfy the equation.
Therefore, NOT a single ordered pair satisfies the equation.