Answer:
1) Combine the x tiles to get:
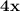
2) Combine integer tiles to get: 3
3) The equivalent function is:
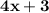
4) If we Substitute any value of x both expressions will be equivalent
Explanation:
We are given expression:
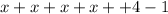
We need to complete following statements.
1) Combine the x tiles to get:
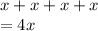
Combine the x tiles to get:
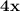
2) Combine integer tiles to get:
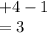
Combine integer tiles to get: 3
3) The equivalent function is:
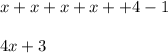
The equivalent function is:
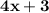
4) If we Substitute any value of x both expressions will be equivalent
Verifying:
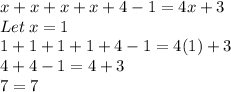
So, Both expressions are equivalent.