Answer:
Option (3)
Explanation:
Given expression represents the sum of k terms of a geometric sequence.
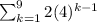
Since, formula to calculate the sum of a geometric sequence is given by,
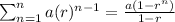
By this formula,sum of 9 terms of the given sequence will be,
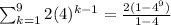
Therefore, Option (3) will be the answer.