Question

Find the domain of the following equations and solve them​

Answer 1

`\boxed{\boxed{\pink{\tt \leadsto The \ domain \ of \ x \ is \ (0,\infty ). }}}`

Explanation:

A equation is given to us and need to find the domain of the equation . So , given equation is ,

`\bf\implies x^(0.5\:log\ x ) = 0.01x^2`

Now , let's simplify this equation to find the domain of x .

`\bf\implies x^(0.5\:log\ x ) = 0.01x^2 \\\\\bf\implies x^(0.5\:log\ x ) -0.01x^2 =0 \\\\\bf \implies x^{log \:x^{(1)/(2)}} - 0.01x^2=0 \\\\\bf\implies x^(log \ √(x)) - 0.01x^2=0`

Now set the argument in log( √x) Greater than or equal to zero to see where the expression is defined. Since the value of log is non - negative.

`\bf\implies √(x) > 0 \\\\\bf\implies (√(x))^2>0^2 \\\\\bf\implies x>0\\\\\bf\implies \boxed{\red{\bf x \in ( 0, \infty ) }}`

In set builder Notation we can write as ,

`\boxed{\red{\bf \ x > 0 \ }}`

Hence the domain of x is ( 0 , ∞ ) .

Answer 2

Domain → x > 0

Solution → x = 100

Explanation:

Given equation is,

`x^{0.5\text{logx}}=0.01x^2`

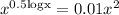
Since, log of any number 'x' is defined when x > 0

Therefore, domain of the equation → x > 0

By taking log on both the sides of the equation,

`\text{log}(x^{0.5\text{logx}})=\text{log}(0.01x^2)`

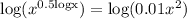
0.5(logx)(logx) = log(0.01) + log(x²)

0.5(logx)²= -2 + 2log(x)

Let log(x) = a

Then the equation becomes as,

0.5a² = -2 + 2a

0.5a² - 2a + 2 = 0

a² - 4a + 4 = 0

(a - 2)² = 0

a = 2

Since, a = log(x)

log(x) = 2

x = 10²

x = 100

Therefore, solution of the given equation is x = 100.