Answer:
Exact Distance =
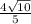
Approximate Distance = 2.529822
============================================
Step-by-step explanation:
This process is quite involved if you don't know the shortcut formula. I'll go over the long method first, and then show the shortcut in the next section.
First we'll need the equation of the line through points O and M. Use of the slope formula will show line OM has slope -1/3, which you are correct in stating.
Then use point slope form to determine the equation of line OM is y = (-1/3)x+11/3. This converts to the standard form x+3y = 11.
For anything in the form Ax+By = C, the equation perpendicular to this is of the form Bx-Ay = D. The A,B coefficients swap, and one item is negated. This helps form the negative reciprocal slope needed for the perpendicular line.
Compare x+3y = 11 to Ax+By = C. We see that A = 1 and B = 3.
So Bx-Ay = D turns into 3x-y = D. Then plug in the coordinates of H(-3,2) and compute to get
3x-y = 3(-3)-2 = -9-2 = -11. So D = -11
The equation 3x-y = D turns into 3x-y = -11 which is the equation of the line through point H and this line is perpendicular to line OM.
At this point, we have this system of equations
x+3y = 11
3x-y = -11
Solve that system however you wish. Substitution may be the best choice. Doing so leads to the intersection point (-2.2, 4.4)
The last step is to apply the distance formula between the points H(-3,2) and the intersection point (-2.2, 4.4)
The distance you should get is
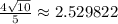
I'm skipping steps because listing everything out would take up way too much space in my opinion.
--------------------------------------------------------
The first section goes over a fairly lengthy process of finding the perpendicular distance. Luckily, there's a shortcut.
Consider an equation of the form Ax+By=C, aka standard form. Now consider a point P located at (m,n) that is not on the line Ax+By = C. We can find the distance from P to the line using this formula below
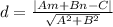
In this case, A = 1, B = 3 and C = 11 found back in the previous section. So you'll still need to calculate the equation of line OM.
Also, we'll use (m,n) = (-3,2) which are the coordinates of point H
From here it's a fairly straightforward computation
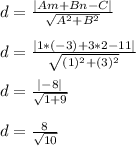
Optionally we can rationalize the denominator like so
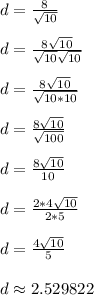
There are different ways to write down the answer, but they all represent the same number.