Question

A student claims that more than 55% of the mothers with school-age children worked outside the home. The student finds that a sample of 150 mothers from Bronx New York revealed that 96 were working outside the home. At a significance level of = 0.05, is the student correct?

Answer 1

There is sufficient evidence that the students claim is correct.

Explanation:

From the information given:

The population proportion P = 55% = 0.55

The sample size n = 150

The sample mean x = 96

The sampling proportion from the sample mean
`\hat p = (x)/(n)`

`\hat p = (96)/(150)`

`\hat p =0.64\\`

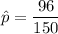
The null and alternative hypothesis is:

`H_o : p = 0.55 \\ \\ H_1 : p > 0.55`

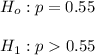
The test statistics can be computed as follows:

`Z = \frac{\hat p - p}{\sqrt{(p(1-p))/(n)}}`

`Z = \frac{0.64 - 0.55}{\sqrt{(0.55(1-0.55))/(150)}}`

`Z = \frac{0.09}{\sqrt{(0.2475)/(150)}}`

`Z = (0.09)/(√(0.00165))`

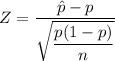
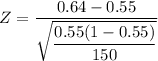
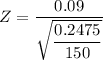
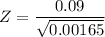
Z = 2.22

The P - value = P ( Z > 2.22)

= 1 - P( Z < 2.22)

= 1 - 0.98679

= 0.01321

Since P-value is less than the level of significance ∝ = 0.05

We reject the null hypothesis
`H_o`

Conclusion: There is sufficient evidence that the students claim is correct.