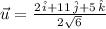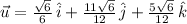Answer:
Magnitude:
 , Direction (unitized):
, Direction (unitized):
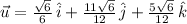
Step-by-step explanation:
Let
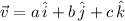 . The magnitude of the vector is represented by the Pythagorean formula:
. The magnitude of the vector is represented by the Pythagorean formula:
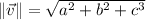 (1)
(1)
And the direction is represented by the direction cosines, measured in sexagesimal degrees, that is:
 (2)
(2)
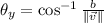 (3)
(3)
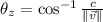 (4)
(4)
If we know that
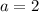 ,
,
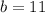 and
and
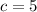 , then the magnitude and directions of the vector are, respectively:
, then the magnitude and directions of the vector are, respectively:
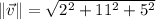

The direction can be represented by the following unit vector:
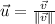 (5)
(5)