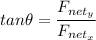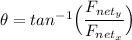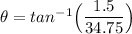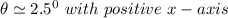Question

In a different tug of war, one team pulls with a force of 50 newtons at an angle of 30 degrees from the positive x-axis, and a second team pulls with a force of 25 newtons at an angle of 250 degrees. Use a scale drawing to determine the total force and angle applied to the central ring. How did they get the following answer?34.8 N at 2.5 degrees from the positive x-axis

Answer 1

34.8 N at 2.5 degrees from the positive x-axis

Explanation:

From the given information:

The force F makes an angle A with the positive x axis can be expressed in terms horizontal and vertical components.

`F_x = F cos A\\\\ F_y = Fsin A`

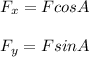
Given that

`F_1 = 50 \ N`

`\theta_1 = 30 ^0 \ \ \ (x-axis)`

`F_(1x) = F_1 * Cos A_1`

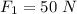
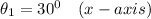
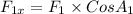
= 50 × cos 30

= 43.3 N

`F_(1y) = F_1 * Sin \ A_1`

= 50 × sin 30

= 25 N

Similarly;

`F_2 = 25 \ N`

`\theta_2 = 250 ^0 \ \ \ ( x-axis)`

`F_(2x) = F_2 * cos \ A_2`

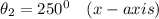
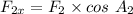
= 25 × cos 250

= - 8.55 N

`F_(2y) = F_2 * A_2`

= 25 × sin 250

= -23.5 N

The total net force;

`F_(net) = F_((net))_x + F_((net))_y`

`F_(net) = (F_(1x) + F_(2x) ) i + (F_(1y) + F_(2y) )j`

`F_(net) = (43.3 - 8.55) i + (25-23.5 ) j`

`F_(net) =34.75 i + 1.5 j`

`|F_(net) | = \sqrt{F_(net)_x^2 + F_(net)_y^2}`

`|F_(net) | = √(34.75^2 + 1.5^2)`

`|F_(net) | = 34.8 \ N`

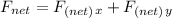
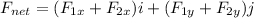
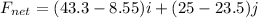
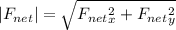
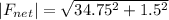
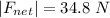
Finally, the direction of the angle for the net force is:

`tan \theta = (F_(net_y))/(F_(net_x))`

`\theta = tan^(-1) \Big ((F_(net_y))/(F_(net_x)) \Big)`

`\theta = tan^(-1) \Big ((1.5)/(34.75)} \Big)`

`\theta = tan^(-1)( 0.043165)`

`\theta \simeq 2.5^0\ with \ positive \ x-axis`