Question

In a group of 100 students, 40 like Computer Science (group A), 30 like Philosophy

(group B), and 20 like both (group A∩B). If a student chosen randomly likes Computer
Science, what is the probability that they also like Philosophy?

Answer 1

Given:

Total number of student = 40

Students who like Computer Science (group A) = 40

Students who like Philosophy (group B) = 30

Students who like both (group A∩B) = 20

To find:

If a student chosen randomly likes Computer Science, what is the probability that they also like Philosophy?

Solution:

Let the following events,

A: Student like Computer Science

B: Student like Philosophy

Now,

`P(A)=(40)/(100)=0.4`

`P(B)=(30)/(100)=0.3`

`P(A\cap B)=(20)/(100)=0.2`

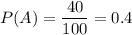
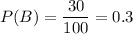
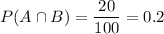
We need to find the probability that the student like Philosophy if it is given that he likes Computer science, i.e,
`P((B)/(A))`.

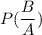Using conditional probability, we get

`P((B)/(A))=(P(A\cap B))/(P(A))`

`P((B)/(A))=(0.2)/(0.4)`

`P((B)/(A))=(1)/(2)`

`P((B)/(A))=0.5`

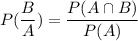
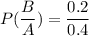
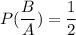
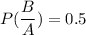
Therefore, the required probability is 0.5.