Answer:
x = 0.0734 m = 7.34 cm
Step-by-step explanation:
First we shall calculate the area of the piston:
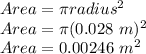
Now, we will calculate the force on the piston due to atmospheric pressure:
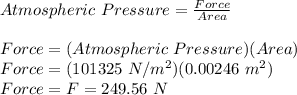
Now, for the compression of the spring we will use Hooke's Law as follows:
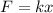
where,
k = spring constant = 3400 N/m
x = compression = ?
Therefore,
x = 0.0734 m = 7.34 cm