Question

A random sample of 144 observations has a mean of 20. The population standard deviation is known to equal 4.8. The 95.44% confidence interval for the population mean is

Answer 1

The population mean is 19.2 to 20.8.

Explanation:

The formula of Confidence interval is

CI = mean ± z*
`(s)/(√(n) )`

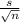
where

n = sample size

s = Population standard deviation.

mean = Sample mean

z(α/2) = Two tailed z-value for significance level of .

Given : Confidence level = 95.44% = 0.9544

Significance level = α = 1-0.9544 = 0.0456

Now we Use standard z-value table

z-value for Significance level of 0.0456 :

z(α/2) = z(0.0228) = 1.99 = 2(approximately)

And we are given

n=144

s = 4.8

mean = 20

so the required Confidence interval is

CI = 20± 2*
`(4.8)/(√(144) )`

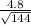
= 20 ± 2*
`(4.8)/(12)`

= 20 ± (0.8)

= (20-0.8, 20+0.8 )

= (19.2 , 20.8)

Therefore the 95.44% CI value for the population mean of 20 is 19.2 to 20.8.