Question

Given two objects represented by the tuples (22, 1, 42, 10) and (20, 0, 36, 8):(a)Compute the Euclidean distance between the two objects. (b) Compute the Manhattan distance between the two objects.

Answer 1

(a) 6.708

(b) 11

Explanation:

Tuples ( 22, 1, 42, 10) and (20, 0, 36, 8)

Euclidian distance formula

`D = √((q1 -p1)^2 + (q2-p1)^2 + (q3 - p3)^2 + (q4 -p4)^2)`

D =
`√((22-20)^2 + (1-0)^2 + (42 -36)^2 + (10 -8)^2 )`

=
`√((2)^2 + (1)^2 + (6)^2 + (2)^2)`

=
`√(4 + 1 + 36 + 4 )`

=
`√(45)`

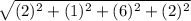
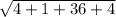
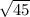
D = 6.708

Therefore the Euclidean distance between the tuples is 6.708

Manhattan Distance formula

D = |q1-p1| + |q2 -p2| + |q3 -p3| + |q4-p4|

= |22-20| + | 1-0| + | 42 -36| + | 10-8|

= |2| + |1| + |6| + |2|

D = 11

Therefore the Manhattan distance is equal to 11