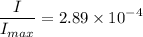Solution :
The expression for the intensity of light is given by :
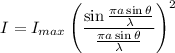
For a small angle, θ
sin θ = tan θ
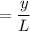
Therefore the above equation becomes,
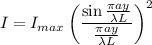
The given data is
λ = 546.1 nm
L = distance between the slit and the screen = 140 cm
= 1.40 m
a = width of the slit
=
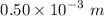
Therefore,
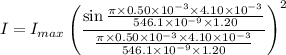
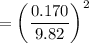
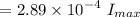
Therefore the fractional intensity is