Question

Consider a population with 3 observations: 6, 10 and 12. You use simple random sampling without replacement to select a sample of 2 observations. What is the probability that the sample mean is larger than 8?

Answer 1

`(2)/(3)`

Explanation:

Given that:

The number of observations is:

6, 10, 12

If we are to use a simple random sampling without replacement, then we will have:

(6,10) (6,12) (10,12)

Here;

the sample size n = 2

The population size N = 3

For (6,10) ; The sample mean =
`(6+10)/(2)`

=
`(16)/(2)`

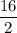
= 8

For (6,12) ; The sample mean =
`(6+12)/(2)`

=
`(18)/(2)`

= 9

For (10, 12) ; The sample mean =
`(10+12)/(2)`

=
`(22)/(2)`

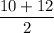
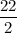
= 11

The probability distribution of sample mean(x) is:

X 8 9 11

P(X=x)
`(1)/(3)`
`(1)/(3)`
`(1)/(3)`

Thus, the probability that the sample mean is larger than 8 is:

P(X> 8) = P(X = 9) + P(X + 11)

P(X> 8) =
`(1)/(3)+(1)/(3)`

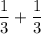
P(X > 8) =
`(1+1)/(3)`

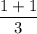
P(X> 8) =
`(2)/(3)`