Question

51. The radius of gold is 144 pm and the density is 19.32 g/cm3. Does elemental gold have a face-centered cubic structure or a body-centered cubic structure

Answer 1

Elemental gold to have a Face-centered cubic structure.

Step-by-step explanation:

From the information given:

Radius of gold = 144 pm

Its density = 19.32 g/cm³

Assuming the structure is a face-centered cubic structure, we can determine the density of the crystal by using the following:

`a = √(8) r`

`a = √(8) * 144 pm`

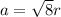
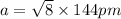
a = 407 pm

In a unit cell, Volume (V) = a³

V = (407 pm)³

V = 6.74 × 10⁷ pm³

V = 6.74 × 10⁻²³ cm³

Recall that:

Net no. of an atom in an FCC unit cell = 4

Thus;

`density = (mass)/(volume)`

`density = ( 4 \ atm ( 196.97 \ g/mol) ((1 \ mol )/(6.022 * 10^(23) \ atoms)))/(6.74 * 10^(-23) \ cm^3)`

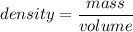
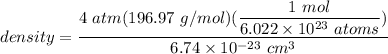
density d = 19.41 g/cm³

Similarly; For a body-centered cubic structure

`r = (√(3))/(4)a`

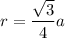
where;

r = 144

`144 = (√(3))/(4)a`

`a = (144 * 4)/(√(3))`

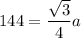
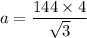
a = 332.56 pm

In a unit cell, Volume V = a³

V = (332.56 pm)³

V = 3.68 × 10⁷ pm³

V 3.68 × 10⁻²³ cm³

Recall that:

Net no. of atoms in BCC cell = 2

∴

`density = (mass)/(volume)`

`density = ( 2 \ atm ( 196.97 \ g/mol) ((1 \ mol )/(6.022 * 10^(23) \ atoms)))/(3.68 * 10^(-23) \ cm^3)`

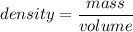
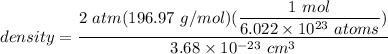
density =17.78 g/cm³

From the two calculate densities, we will realize that the density in the face-centered cubic structure is closer to the given density.

This makes the elemental gold to have a Face-centered cubic structure.