Answer:
The number which should be added with 49x square + 4y square to get a perfect square is 28xy
Explanation:
We need to find the number which is to be added with 49x square + 4y square to get a perfect square.
The expression given is:
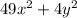
For the expression to be perfect square it should be of form:
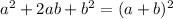
Now, we are given
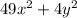 and we need to find the middle term
and we need to find the middle term
So, solving:

The number which should be added with 49x square + 4y square (
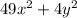 ) to get a perfect square is 28xy
) to get a perfect square is 28xy