Question

X is normally distributed random variable with mean 63 and standard deviation 6, the probability that X lies between 45 and 81 is

Answer 1

P(45<X<81) = P(-3<z<3)=0.9974 or 99.74%

Explanation:

Mean = 63

Standard Deviation =6

We need to find probability that X lies between 45 and 81 i.e P(45<X<81)

First we will find z-score for X=45 and X=81

For X=45 the z-score can be found using formula:
`z-score=(X-\mu)/(\sigma)`

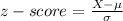
Putting values and finding z-score

`z-score=(X-\mu)/(\sigma)\\z-score=(45-63)/(6)\\z-score=-3`

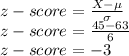
For X=45, z-score is -3

For X=81 the z-score can be found using formula:
`z-score=(X-\mu)/(\sigma)`

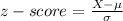
Putting values and finding z-score

`z-score=(X-\mu)/(\sigma)\\z-score=(81-63)/(6)\\z-score=3`

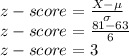
For X=81, z-score is 3

Now finding the probability of P(-3<z<3)

It can be solved as:

P(-3<z<3)=P(z<3)-P(z<-3)

Looking at the z-score table to find

P(z<3)= 0.9987

P(z<-3)=0.0013

So, P(-3<z<3)=P(z<3)-P(z<-3)

P(-3<z<3)=0.9987 - 0.0013

P(-3<z<3)=0.9974

or P(-3<z<3)= 99.74%

So, P(45<X<81) = P(-3<z<3)=0.9974 or 99.74%